In machine learning, it is generally assumed that the training samples are Independent and Identically Distributed (IID). As far as the sequence data is concerned, this isn't always true. If the sequence values have temporal dependence among them, such as Time Series data, the IID assumption fails.
The sequence modelling algorithms hence come in two flavours, Stateless and Stateful, depending upon the architecture used while training. Following is a discussion using LSTM as an example, but the notion is applicable to other variants as well namely RNN, GRU etc.
Stateless
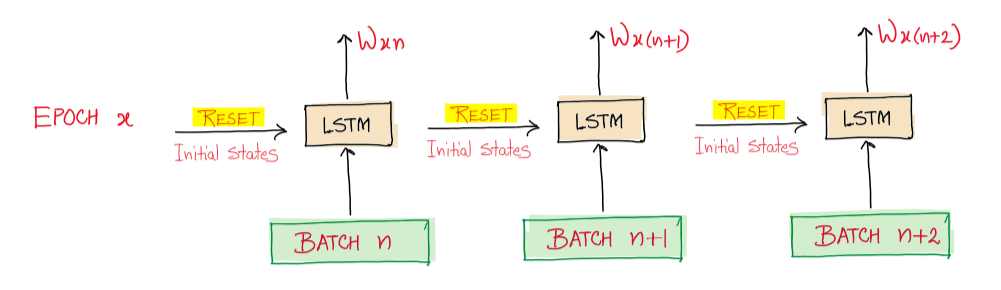
This architecture is used when the IID assumption holds. While creating batches for training, this means that there is no inter-relationship across the batches and each batch is independent from one another.
The way these the two architectures differ is the manner in which the states (cell and hidden states) of the model (corresponding to each batch) are initialized as the training progresses from one batch to another. This is not to be confused with the parameters / weights, which are anyways propagated through the entire training process (which is the whole point of training)
In the above diagram, the initial states of LSTM are reset to zeros every time the new batch is taken up and processed, thus not utilizing the already learned internal activations (states). This forces the model to forget the learnings from previous batches.
Stateful
Sequence data such as Time Series contains non-IID samples, and hence it won't be a good idea to assume that the divided batches are independent, when they are actually not. Hence it is intuitive to propagate the learned states across the subsequent batches, so that the model captures the temporal dependence not only within each sample sequence but across the batches too.
(Note that for text data, where a sentence represents a sequence, it is generally assumed that the corpus is made up of independent sentences, with no connection between them. Hence, it is safe to go for stateless architecture. Whenever this assumption doesn't hold true, Stateful is to be preferred.)
Below is how a Stateful LSTM architecture looks like.
Here, the cell and hidden states of LSTM for each batch, are initialized using the learned states from the previous batch, thereby making the model learn the dependence across the batches. The states are however reset, at the start of each epoch.
A more fine grained visualization showing this propagation across the batches is shown below:
Here the state of the sample located at index i, X[i] will be used in the computation of the sample X[i+bs] in the next batch, where bs is the batch size. More precisely, the last state for each sample at index i
in a batch will be used as initial state for the sample of index i in the following batch. In the diagram, the
length of each sample sequence is 4 (timesteps) and the values of LSTM states at timestep t=4 are used for
initialization in the next batch.
Observations:
1. As the batch size increases, Stateless LSTM tends to simulate Stateful LSTM.
2. For Stateful architecture, the batches are not shuffled internally (which otherwise is the default step in case of stateless ones)
(Note that for text data, where a sentence represents a sequence, it is generally assumed that the corpus is made up of independent sentences, with no connection between them. Hence, it is safe to go for stateless architecture. Whenever this assumption doesn't hold true, Stateful is to be preferred.)
Below is how a Stateful LSTM architecture looks like.
Here, the cell and hidden states of LSTM for each batch, are initialized using the learned states from the previous batch, thereby making the model learn the dependence across the batches. The states are however reset, at the start of each epoch.
A more fine grained visualization showing this propagation across the batches is shown below:
in a batch will be used as initial state for the sample of index i in the following batch. In the diagram, the
length of each sample sequence is 4 (timesteps) and the values of LSTM states at timestep t=4 are used for
initialization in the next batch.
1. As the batch size increases, Stateless LSTM tends to simulate Stateful LSTM.
2. For Stateful architecture, the batches are not shuffled internally (which otherwise is the default step in case of stateless ones)
References:
Comments
Post a Comment