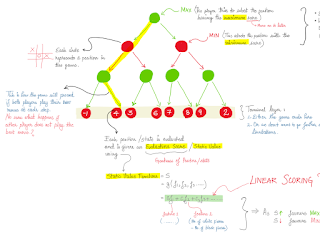
Minimax is an algorithm in game theory to find the optimal move for a player, assuming that your opponent also plays optimally. It is widely used in two player turn-based games such as Tic-Tac-Toe, Backgammon, Mancala, Chess, etc.
The data structure used to visualize the game progression is called "Game Tree" and looks like the one shown below. Each level in the game tree represents all the possible moves available to the player at that turn.
The name "MiniMax" is derived from "Min" and "Max", the two participating players, who try to play the most optimum moves on their turn. "Max" on each of its turn tries to play the move that maximizes the state value function. "Min" on the other hand tends to minimize this value. Its important to note here that the game tree corresponding to a particular game is drawn beforehand. Minimax algorithm is just a way to traverse through it (in a depth first search fashion) in such a way that the player (Min/Max) who plays the first move wins it.
The state value function is a method (linear scoring polynomial) to evaluate the goodness of the terminal state of the game from the perspective of Max. Greater is the value of this function, more it favours Max. Min on the other hand tries to minimise this value, essentially meaning that the opponent is playing the best possible move against Max.
1. Either the game ends here
2. Or its not possible to further grow the tree because of computational constraints (huge number of possible moves)

But what if the game tree is huge. It might not be feasible to traverse each and every possible subtree of every possible move. The needed optimization is done through Alpha-Beta pruning which is an optimization technique for Minimax. It reduces the computation time by a huge factor. This allows us to search much faster and even go into deeper levels in the game tree. It cuts off branches in the game tree which need not be searched because there already exists a better move available. It is called Alpha-Beta pruning because it passes 2 extra parameters in the minimax function, namely alpha and beta.
Let’s define the parameters alpha and beta.
Alpha is the best value that the maximizer currently can guarantee at that level or above.
Beta is the best value that the minimizer currently can guarantee at that level or above.
Finally, there is an important assumption that the human players play optimal moves at each step. If not, the algorithm will fail. Hence, you might be better off not using this algorithm against a not-so-intelligent/dumb human opponent.
Reference:
Search: Games, Minimax, and Alpha-Beta (MIT Lecture)


Comments
Post a Comment