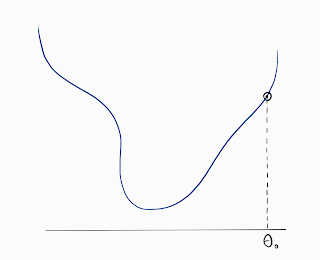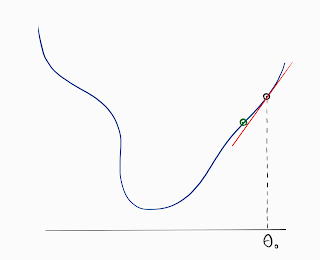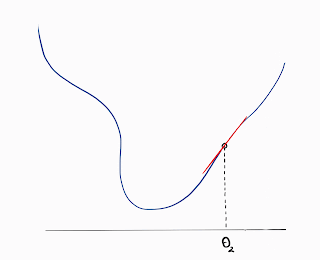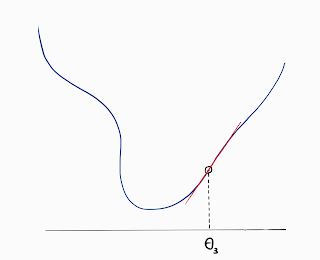
Optimization is at the core of Machine Learning. The goal is to minimize a loss function by iteratively varying the weight parameters. Weights at each of those optimization steps get updated as shown in the following figure.
The theta_step in the above equation depends on how the loss function is approximated at θ: Linear or Quadratic.
But why do we need function approximation?
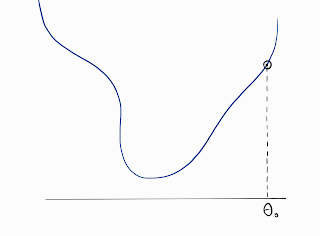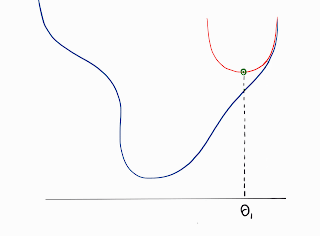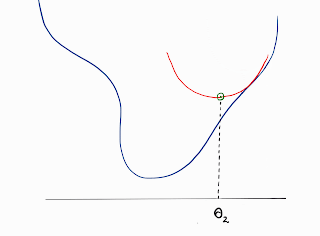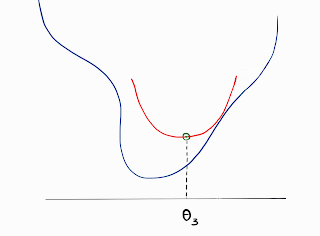
The given loss function could be a complex one. To avoid complex calculations pertaining to the loss function, we generally estimate the original function using a series of polynomial functions which are easier to evaluate. This is done using the Taylor Series.

Once the function is approximated, theta_step is derived and is known as:
- Gradient Step if it was approximated as a linear function.
- Newton Step if approximated as a quadratic function.
These approaches are therefore known as Gradient Descent and Newton's Method respectively.
(The mathematics behind this derivation can be found here)
The final equation for both the methods is shown below:
Fact: If Newton's Method is used on the square of error in Linear Regression then the optimal coefficients are obtained in one step only.
Intuition: In second-order function approximation for a function f(𝜽),
where F is the approximated function.
Since, the loss function - square of errors, is perfectly quadratic and convex, the approximated function will overlap with the original function for any given 𝜽.
References:




Comments
Post a Comment